LOOPS E RECURSÃO: EFICIÊNCIA E APLICAÇÕES
~10 min. de leitura
Guilherme Faura, 15/07/2024
Aprenda sobre Recursão, o que é, como funciona, aplicações, algumas curiosidades e veja também um comparativo sobre recursividade vs estruturas de repetição convencionais.
Computacionalmente, quando fazemos algum algoritmo e tratamos estruturas de dados no processo, muitas vezes precisamos de uma forma de repetição para realizar certas operações.
Tradicionalmente a forma que estamos familiarizados a fazer é através de funções for() ou while() (e suas variantes) em linguagens de família-C. Como nos dois exemplos a seguir:
#include <stdio.h>
int main() {
int vec[5] = {0, 1, 2, 3, 4}; // Vetor genérico representando os dados
printf("{");
// Imprimindo cada elemento do vetor...
for(int i = 0; i < 5; i++) {
printf("%d ", vec[i]);
}
printf("}");
return 0;
}
#include <stdio.h>
int main() {
int vec[5] = {0, 1, 2, 3, 4}; // Vetor genérico representando os dados
printf("{");
int i = 0;
// Imprimindo cada elemento do vetor...
while(i < 5) {
printf("%d ", vec[i]);
i++;
}
printf("}");
return 0;
}
Mas você sabia que essas não são as únicas formas de se processar dados? Na verdade, muitas linguagens de programação nem possuem loops baseados em for() ou while() ou suas variantes. Isso foi popularizado pela linguagem C, criada em 1972, e, seu grande sucesso de sua época influenciou o mundo das linguagens de programação posteriores, tais como C++, Java, PHP e C#, que também adotaram sintaxes muito parecidas, criando familiaridade e adoção entre programadores.
Na própria linguagem C, há ainda uma outra forma de se fazer repetições, esta é chamada de recursão. Recursão ou recursividade é um processo na qual um trecho de código pode chamar a si mesmo dentro do seu próprio escopo, repetindo uma operação, por exemplo, uma função que em sua declaração chama a si mesmo em determinado momento — assim, sendo possível de se fazer uma repetição sem de fato precisar utilizar formas tradicionais de repetições, apenas variando os parâmetros sendo passados na função a cada execução. Vejamos um exemplo em C de recursividade reescrevendo a partir dos mesmos exemplos mostrados anteriormente:
#include <stdio.h>
void imprimir_vetor(int vetor[], int tamanho, int indice) {
if(indice == tamanho) {
return;
}
printf("%d ", vetor[indice]);
imprimir_vetor(vetor, tamanho, indice + 1);
}
int main() {
int vetor[5] = {0, 1, 2, 3, 4}; // Vetor genérico representando os dados
printf("{");
imprimir_vetor(vetor, 5, 0); // Chamando a função recursiva
printf("}");
return 0;
}
Note que, em nenhum momento foram utilizadas estruturas de repetições tradicionais da linguagem C para isso, somente recursividade. Observe que temos uma função externa da main chamada imprimir_vetor() que recebe 3 parâmetros (vetor, tamanho, indice), onde vetor seria sua própria estrutura de dados sendo passada, que neste caso é um vetor simples, tamanho seria o tamanho do seu vetor, 5 neste caso e, indice seria uma variável para controlar o índice da sua operação similarmente quando você tem as estruturas de repetições que passam por cada elemento acessando os dados através de índices (geralmente chamados de i).
Chamamos na main a função imprimir_vetor() passando como parâmetros nosso vetor, seu tamanho e o numero inicial para o índice, sendo então imprimir_vetor(vetor, 5, 0);. Assim, na nossa função, que recebe esses parâmetros, primeiro fazemos uma checagem se o índice e o tamanho são iguais pelo seguinte motivo:
- Para checar a condição de término do processo. Porque por mais que a função seja do tipo void (a principio sem retorno de nada, já que só está sendo impresso os dados), com essa condição é possível de saber quando a operação termina por completo e então, quando terminar, fazer um return; (vazio mesmo), justamente para quebrar o fluxo e terminar.
Em seguida, é possível de se analisar a recursividade acontecendo de fato. Primeiro é impresso o elemento na qual o índice se encontra direto, em seguida, é chamado a função novamente, com os mesmos parâmetros do vetor e o seu tamanho, exceto que, ao passar a variável do índice, é incrementado o índice em 1.
O que acontecerá é que a função imprimir_vetor() será executada novamente, mas desta vez com o índice agora começando de 1 ao invés de 0, sendo esta então a segunda vez que a função está sendo executada e a mesma coisa será realizada posteriormente repetidamente até que o índice se torne numericamente de mesmo valor do tamanho do vetor, no nosso caso 5. E quando isso acontecer, significa que o processo terminou e o fluxo será quebrado com o return;.
Repare também que, a chamada da recursão ocorre na ultima linha de execução da função imprimir_vetor(). Isto é chamado de “Recursão de Cauda”, ou seja, quando a recursividade é efetuada na ultima declaração de uma função e é a última execução de fato, em outras palavras, quando não resta mais nada para ser executado. E a Recursão de Cauda é especial, pois, muitos compiladores fazem otimizações pesadas para este tipo especifico de recursão visando também evitar o estouro de pilha (no fundo convertendo-os para loops convencionais de forma que se tornem mais eficientes em termos de performance) — mas isso nem sempre é possível e nem todas as linguagens de programação fazem. O que geralmente não acontece para uma “função recursiva sem cauda” (quando a recursividade não é feita como a última execução de uma função), sendo ainda mais “custosa” em termos de desempenho.
Muito interessante né? De fato algumas outras linguagens de programação, tais como Lisp, Scheme, Prolog e Haskell não usam formas tradicionais de repetições como as que estamos familiarizados, mas na verdade, por possuírem paradigmas de programação diferentes, utilizam conceitos recursivos em suas operações.
Mas, existem certos detalhes sobre recursão, que podemos explorar ainda mais a fundo e fazermos uma comparação para reflexão de suas vantagens e desvantagens.
A principal vantagem a priori da recursividade seria, talvez que, ela endorsa uma certa “modularidade natural” no código, em outras palavras, para que ela funcione corretamente, é necessário que o desenvolvedor torne o código mais modular, escrevendo funções externas, como demonstrado no exemplo acima. Essa “modularidade natural” permite uma organização e separação de trechos de códigos em blocos externos menores que podem ser reutilizáveis ao decorrer do sistema — um principio fundamental das boas praticas de programação.
No entanto, a recursividade traz consigo também desvantagens, sendo estas, principalmente relacionadas com desempenho e legibilidade…
Tratando-se primeiramente sobre desempenho, imagine que a cada nova chamada da função há um custo de performance associado, cada chamada recursiva gera um quadro de pilha (stack frame) onde os parametros da função são copiados, o que pode gerar um custo excessivo para a memória. No exemplo exposto existem poucos parâmetros — um simples vetor, com somente 5 elementos numéricos dentro, um inteiro para tamanho e outro inteiro para o índice — mas imagine um caso real com uma grande quantidade de dados para ser processada e uma função com mais parâmetros, observe que uma função inteira com seus parâmetros estão sendo alocados na memoria de novo e de novo, sendo continuamente copiadas para a memoria para cada “vez da repetição” (cada chamada gerando um novo quadro de pilha com o endereço de retorno, variáveis locais e parâmetros da função). Note que, em C, ao passar arrays para funções, passamos apenas o ponteiro para o array, não uma cópia dos dados. No entanto, os parâmetros e outras variáveis locais são duplicadas em cada quadro de pilha, contribuindo para o uso de memória. Para demonstrar isso, é possível de se fazer até uma análise de um benchmark mínimo (não tão rigoroso e não tão controlado) comparando o desempenho das estruturas de repetição.
(Note que um benchmark mais rigoroso deveria ser realizado em um ambiente (uma máquina) mais controlada, que estivesse sem (ou minimamente sem) muitos processos sendo executados de fundo para não interferir (por exemplo atrasar ou variar) na medição, e também uma maior quantidade de dados para se processar, assim, para se ter resultados mais precisos… Mas, realizando o seguinte benchmark minimo, com um simples programa que soma todos os números de 0 a n, sendo n uma quantidade fixa, neste caso para um n = 10000, já é possível de enxergar o ponto…)
#include <stdio.h>
#include <time.h>
// Função recursiva
int recursiva(int n) {
if (n == 0) {
return 0;
} else {
return n + recursiva(n - 1);
}
}
// Função com loop while
int loop_while(int n) {
int soma = 0;
int i = 0;
while(i <= n) {
soma += i;
i++;
}
return soma;
}
// Função com loop for
int loop_for(int n) {
int soma = 0;
for(int i = 0; i <= n; i++) {
soma += i;
}
return soma;
}
int main() {
int n = 10000;
clock_t start, end;
// Medir tempo de execução da função recursiva
start = clock();
int resultado_recursivo = recursiva(n);
end = clock();
double tempo_recursivo = ((double)(end - start)) / CLOCKS_PER_SEC;
// Medir tempo de execução da função com loop while
start = clock();
int resultado_while = loop_while(n);
end = clock();
double tempo_while = ((double)(end - start)) / CLOCKS_PER_SEC;
// Medir tempo de execução da função com loop for
start = clock();
int resultado_for = loop_for(n);
end = clock();
double tempo_for = ((double)(end - start)) / CLOCKS_PER_SEC;
// Mostrar os resultados
printf("Resultado recursivo: %d\n", resultado_recursivo);
printf("Tempo de execução recursivo: %f segundos\n\n", tempo_recursivo);
printf("Resultado loop while: %d\n", resultado_while);
printf("Tempo de execução loop while: %f segundos\n\n", tempo_while);
printf("Resultado loop for: %d\n", resultado_for);
printf("Tempo de execução loop for: %f segundos\n", tempo_for);
return 0;
}
Ao executarmos, obtemos os seguintes resultados de saída:
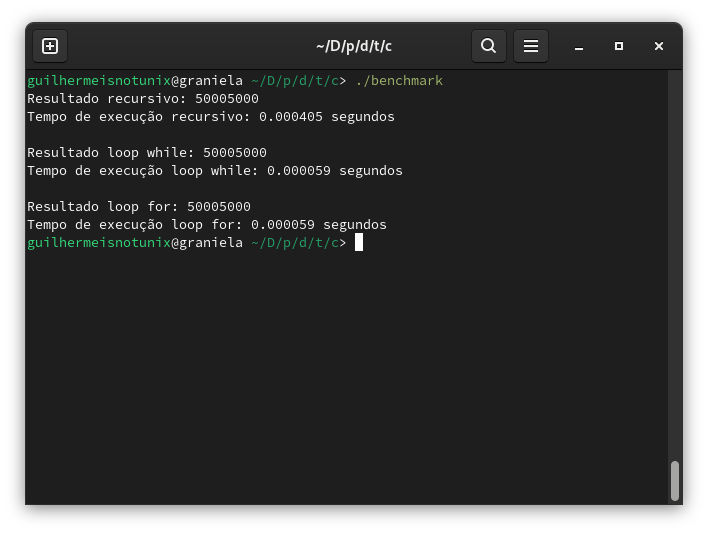
Veja que, ao executar o teste de benchmark, primeiro, todos os resultados das somas foram iguais para o mesmo n fixo, independente do método utilizado, o que mostra que as somas foram realizadas corretamente. Mas, observe a diferença de tempos… Pode-se concluir que: com um benchmark mínimo realizado pôde ser verificado que os tempos dos loops for() e while() foram iguais (e ao executar várias vezes, há uma pequena variação na minha máquina, quase imperceptível entre eles, fazendo com que as vezes o loop for() fosse 0.000001 segundo mais rápido que o while()), enquanto que o tempo da função recursiva sem cauda estivesse aproximadamente 7 vezes mais lento em relação aos outros dois métodos.
Por questões de didática, há uma simplificação omitida neste último exemplo. Foi usado como exemplo acima especificamente uma função recursiva sem cauda — que foi mencionado anteriormente de se tratar do tipo menos otimizado de recursividade — isso foi proposital, justamente para mostrar a diferença... Por mais que pareça uma Recursão de Cauda, a chamada da função estar em sua última linha não significa que ela seja a última coisa a ser executada necessariamente. Repare que, nesse caso, na verdade a chamada da função recursiva não é a última coisa a ser executada de fato pois após a chamada da função recursiva(n - 1) ocorrerá em seguida uma operação pendente de adição n + recursiva(n - 1), assim, sendo então a adição a última coisa a ser executada na prática, portanto não se classificando mais tecnicamente como uma Recursão de Cauda.
Agora, tratando-se de legibilidade, utilizar a recursão também pode não ser ideal. As linguagens usuais, principalmente da família-C, carregam — o que foi mencionado anteriormente sobre — familiaridade. É familiar acompanhar o raciocínio logico de uma repetição baseada em for() ou while(), é intuitivo, enquanto que, o uso da recursão (apesar de geralmente reduzir linhas de códigos) pode confundir programadores que não estão acostumados a acompanhar depurações de funções recursivas ou eles acidentalmente criarem funções recursivas sem condição de parada (sem fim), justamente por não ser tão comum, sendo mais comum em linguagens baseadas no paradigma funcional, como Haskell. Porém, isso pode ser discutível, já que, quando estruturas de repetições convencionais se tornam mais complexas ou mal escritas — quando por exemplo carregam múltiplas condições iterativas — também se tornam complexas para depurações.
No mundo real, principalmente com a ascensão de IAs, recursividade está intimamente relacionado com processamento de linguagem natural, sendo uma forma comum de se analisar e classificar tokens — e pelo mesmo motivo, também é um método comum de aplicação para tokens em compiladores e interpretadores, sendo assim, uma técnica muito utilizada por designers de linguagens de programação. Inclusive, ótimas ideias a serem abordadas aqui neste blog futuramente.
REFERÊNCIAS
[1] KERNIGHAN, B. W.; RITCHIE, D. M. The C programming language.
[2] CORMEN, T. H.; LEISERSON, C. E.; RIVEST, R. L.; STEIN, C. Introduction to Algorithms.
Escrito por Guilherme Faura

Data: 15/07/2024